密码学-公钥密码系统

gong_yz大约 33 分钟安全相关

一、什么是公钥密码系统

文章来源：https://zhuanlan.zhihu.com/p/562371235open in new window

对称加密总是需要加解密双方预先共享或协商好相同的密钥，在很多场景，特别是当今互联网环境下，这是很不安全的。

解决这个问题的一个重要方向就是使用公钥密码学，英文是Public-key cryptography，也叫做非对称式密码学(Asymmetric cryptography)。

公钥密码学需要两个密钥组成具有某种数学对应关系的密钥对，一个叫公钥，一个叫私钥，公钥公开，私钥保密。而基于公私钥，公钥密码学主要提供了三类算法:

  • 数字签名 : 只有消息的发送者(拥有私钥且保密)才能产生的别人无法伪造的一段数字串，这段数字串同时也是对消息真实性的一个有效证明。数字签名类似于人类的签名、公章、手印等，可以保证消息的真实性、完整性和不可否认性，是目前公钥密码学最广泛的用途。数字签名使用私钥签名，使用公钥验签。
  • 密钥协商 : 在不安全的网络通信环境中，确保通信双方安全地协商出一套共享密钥的方法。密钥协商算法能够在通信内容被攻击者截获的情况下，依然协商出一套攻击者无法获知的共享密钥。密钥协商是当前互联网环境下安全通信的关键算法。
  • 非对称加密 : 相对于对称加密的一种加密算法，使用公钥加密，私钥解密。非对称加密相比对称加密更加安全，但效率要低的多，目前实际使用越来越少，比如很多基于椭圆曲线的公钥密码系统甚至不再提供非对称加密算法。

直觉上，解决对称加密共享密钥不安全问题的方式是，直接使用非对称加密，但事实并非如此。 一来，非对称加密效率很低，在通信频率频繁、消息较长等场景下，使用非对称加密很不划算。 另外很重要的一点就是，在互联网这种不安全的网络环境下，每次通信都使用相同的密钥的话，会增加密钥泄露被攻破的风险，最好每次通信会话都生成不同的密钥。 因此，实际上公钥密码学用来解决对称加密共享密钥问题的方法，是在每次通信时，使用密钥协商算法协商一套临时的会话密钥，并结合数字签名做身份验证。这一点会在后续笔记中继续学习。

公私钥的特点是，在目前的数学理论与实际算力的前提下，无法根据公钥计算出私钥。但要注意，私钥一旦泄露，则公钥容易被破解，因此公私钥不可混用。

而能够提供这种公私钥的系统就是公钥密码系统(public-key cryptosystem)，目前最常用的公钥密码系统有RSA和ECC。

  • RSA基于数学上的大整数的因数分解问题，是应用较早，最为普及的公钥密码系统。但它的性能消耗较高，且在保证安全的前提下，所需密钥长度很长。目前业界普遍认为要保持足够的安全强度，RSA的密钥长度需要2048位，即256个字节。RSA目前虽然仍被大量使用，但已经开始慢慢被ECC取代。
  • ECC则基于椭圆曲线离散对数问题，是新一代公钥密码系统的主流趋势，可以认为是RSA的替代者。相比RSA，ECC在提供相同安全强度的前提下，密钥长度只需要256位，即32个字节。此外ECC的运算速度也更快，性能消耗更少，数学理论上的破解难度也更大。

无论RSA还是ECC，其安全性主要建立在数学问题的难以破解上。 即除了暴力破解(以目前的计算机算力而言，实际破解时间无法接受)外，理论上无法在一个合理时间内破解私钥。

万一数学理论发展解决了数学问题，则对应的密码学算法就不再安全；此外，如果有朝一日计算机算力得到极大提升，比如量子计算机进入实用阶段，那么现在看来不合理的暴力破解时间也有可能缩短到一个合理时间内，这样的话，很多目前认为安全的密码学算法也就不安全了。

本篇笔记主要学习ECC的相关密码学算法，包括主流的椭圆曲线及其算法，咱们国家的SM2，开源社区主推的椭圆曲线及其算法，然后在最后了解一下RSA的相关原理与算法。

二、ECC相关算法

首先学习一下ECC是如何产生公私钥的，然后再学习一下基于ECC公私钥的相关密码学算法。

2.1 ECC

ECC就是Elliptic Curve Cryptography，椭圆曲线密码学，是一套主要用于密钥协商、数字签名以及非对称加密等场景下的密码学理论。

2.1.1 椭圆曲线与公私钥

首先ECC所谓的椭圆曲线在数学上就是一个数学方程式，该方程式对应一个椭圆曲线(并不是椭圆)，该曲线上的点由方程式决定。

一条椭圆曲线就是一组被y^2 = x^3 + ax + b定义的且满足公式4a^3+27b^2!=0的点集。这些点连接起来就是一条曲线，但这条曲线并不是一个椭圆，叫椭圆曲线是因为数学上具备椭圆的一些特征。

y^2 = x^3 + ax + b被称为椭圆曲线的维尔斯特拉斯标准形式(Weierstrass Curve)，而4a^3+27b^2!=0这个限定条件是为了保证曲线不包含奇点(singularities)。

一条椭圆曲线，可能长成下面的样子(a=-1.7, b=4.7):

椭圆曲线
椭圆曲线

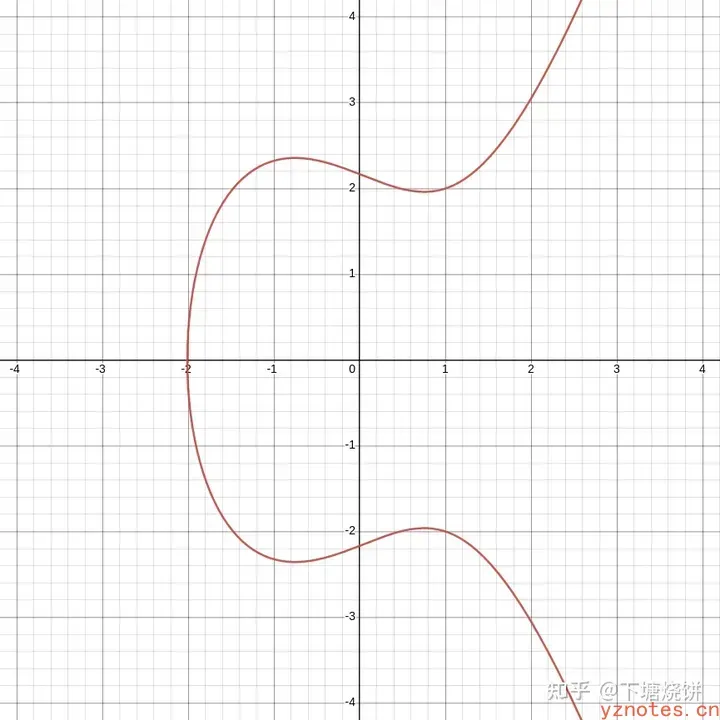
椭圆曲线

随着a,b参数的变化，椭圆曲线的样子也会不同:

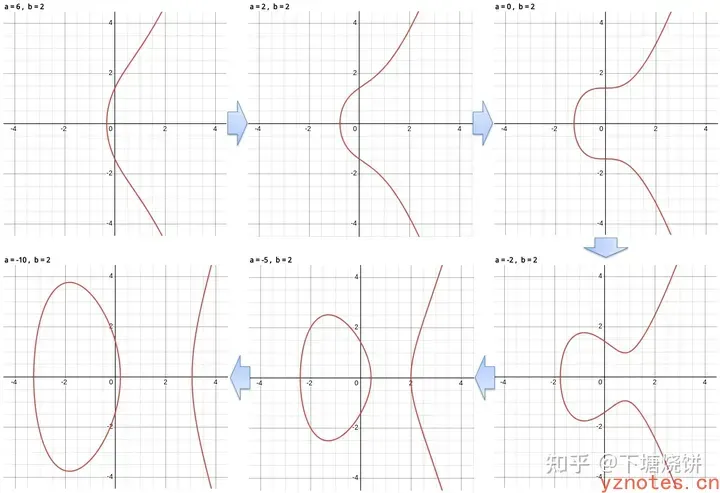
不同参数的椭圆曲线
不同参数的椭圆曲线

不同参数的椭圆曲线

所谓奇点就是不可导的点，此时a,b参数不满足4a^3+27b^2!=0，椭圆曲线变成了下面这样子:

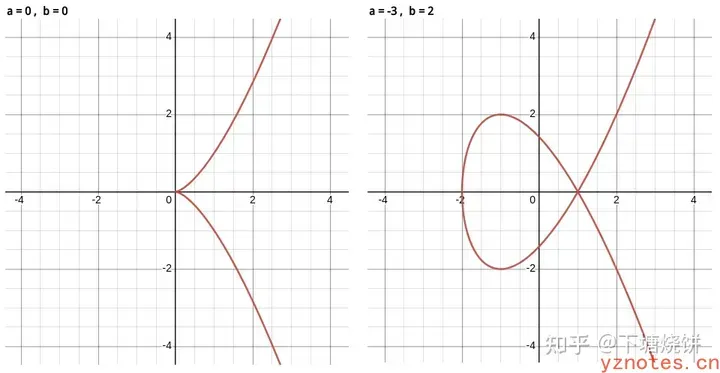
带奇点的椭圆曲线
带奇点的椭圆曲线

带奇点的椭圆曲线

ECC的椭圆曲线不能带有奇点，所以才有 4a3+27b2 != 0 这个限制条件。

在没有奇点的椭圆曲线上，有一种打点操作，是一种几何加法，可以通过曲线上的两个点计算得到第三个点，即P + Q = R，实际就是过P和Q的直线与椭圆曲线会相交于某一点，再对这一点其取曲线上的逆元R点，如下图所示:

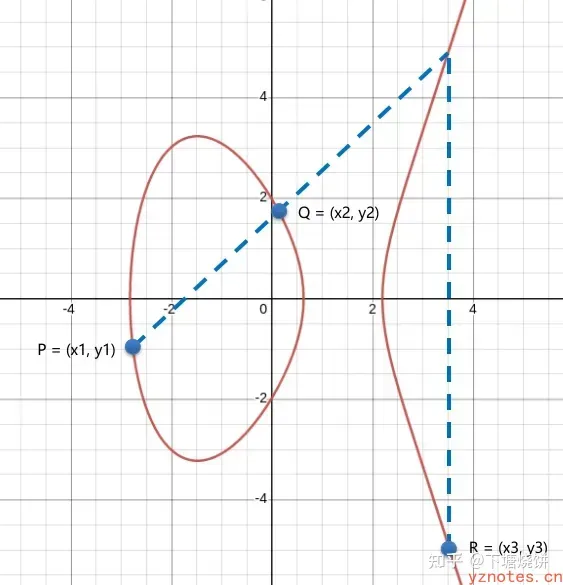
椭圆曲线加法_不同点相加
椭圆曲线加法_不同点相加

椭圆曲线加法_不同点相加

当P和Q重合时，即P + P = R，就是过P点的切线与椭圆曲线会相交于某一点，再对这一点其取曲线上的逆元R点，如下图所示:

img
img

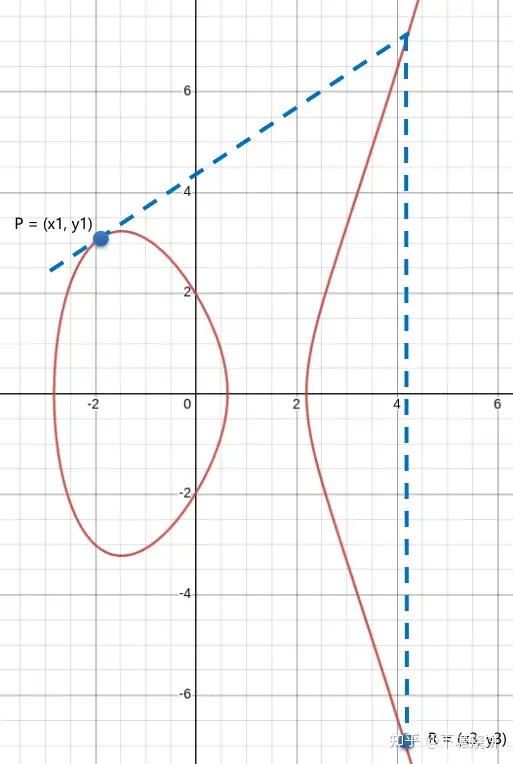
椭圆曲线加法_相同点相加

打点操作需要先在椭圆曲线上选择一个点作为基点G，从这个基点G开始，做G的累加操作，重复d次，就会最终得到椭圆曲线上的另一个点H，即:

G + G + ... + G = d * G = H

这个过程在数学上简化记为 H = d * G。

这里的*不是自然数乘法，而是打点操作的乘法，即代表从G开始的打点操作重复了d次。

例如G * 4的计算就如下图所示:

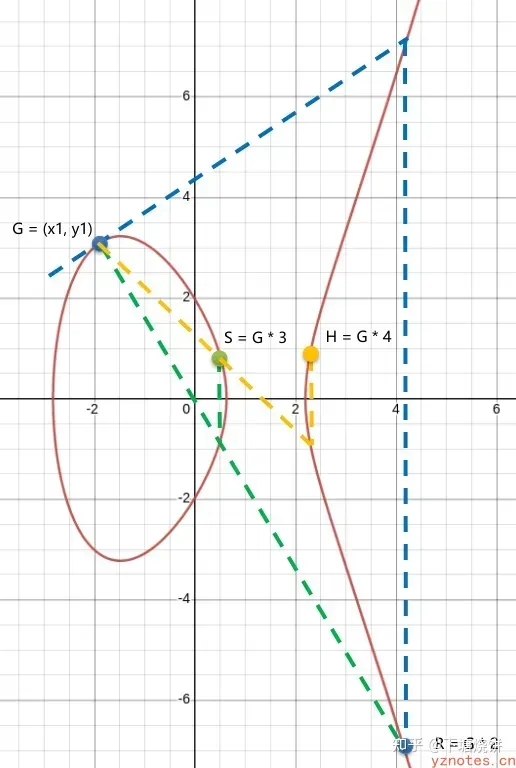
椭圆曲线加法_相同点相加
椭圆曲线加法_相同点相加

椭圆曲线加法_G×4

打点次数d就是私钥，它是一个随机数；最终点H就是公钥，因为是曲线上的一个点，因此有(x,y)两个标量，通常组合成一个数字作为公钥存储和传输。

ECC保证安全的关键就在于，就算知道方程式，基点G，最终点H，也无法知道到底打点了多少次，即无法推算出私钥d，这个就对应数学上的椭圆曲线离散对数难题(ECDLP)。

综上，在使用ECC生成公私钥时，需要先生成一个随机数作为打点次数d，然后就可以从基点G计算出公钥H。这样就生成了公私钥对。

  1. 选取一个[1, n-1]之间的随机数d作为私钥，n即子群阶。(这里获取随机数时应使用CSPRNG)
  2. 通过H=d*G计算公钥。

任意椭圆曲线都可以写为维尔斯特拉斯曲线形式，但除了维尔斯特拉斯曲线，实际上还有其他的椭圆曲线类型，比如蒙哥马利曲线(Montgomery Curve)、扭曲爱德华曲线(Twisted Edwards Curve)等。它们的方程式与维尔斯特拉斯曲线的方程式有所不同，但数学上都可以写为维尔斯特拉斯标准形式。当满足特定条件时，维尔斯特拉斯标准形式可以转换为这些特殊的椭圆曲线形式。 注意，当我们讨论ECC时，大部分情况下特指基于维尔斯特拉斯标准形式的椭圆曲线的相关算法。其他椭圆曲线形式及其相关算法虽然概念上也属于ECC范畴，但它们的算法与ECC相关算法并不完全相同。 这里生成公私钥的算法是基于维尔斯特拉斯标准形式的，其他椭圆曲线比如某些扭曲爱德华曲线的公私钥生成算法与ECC的公私钥生成算法并完全不相同。

从ECC生成公私钥的过程中我们可以看到，ECC的公钥是由私钥推导计算得来，私钥一旦暴露，公钥也就暴露了，因此私钥不可以当作公钥使用。ECC的公钥和私钥在数学上是不一样的，不可以交换使用。

当然ECC不是只用来生成公私钥的，在签名与验签、密钥协商等场景中，还会基于它的打点操作进行公私钥生成以外的算法设计。

目前除了SM2，并没有见到使用ECC实现的非对称加密算法，对ECC的使用主要还是数字签名与密钥协商算法。 ECC当然能够实现非对称加密，推测极少有人设计ECC非对称加密算法的原因，大概是非对称加密的效率很低，没有实际的应用场景。在加密通信场景，都是用密钥交换算法协商出一个或一组密钥，然后使用对称加密算法对消息进行加解密，这样的通信就同时具备安全与高效的特点。 RSA是个特殊情况，它虽然有非对称加密算法，但实际上似乎它的非对称加密算法只是在RSA密钥交换算法里使用。(RSA的密钥交换算法相当简陋，就是基于其非对称加密算法的简单使用，后续会简单介绍。) 而ECC的密钥交换算法在算法设计上与RSA完全不同，根本不需要像RSA那样先实现ECC的非对称加密。 另外还有一些资料，直接将某些椭圆曲线的密钥交换算法称为加密算法，我怀疑是RSA造成的误解: RSA的密钥交换算法就是使用其非对称加密算法，因此被人误解为所有的密钥交换算法都是非对称加密算法。。。

2.1.2 ECC相关参数

ECC生成公私钥时需要先获取一个位于[1, n-1]之间的随机数作为私钥。很明显，这个随机数范围n越大越好，这个范围n实际上是ECC的一个参数，叫子群的阶n，它是由另一个参数素数P通过一定的计算推导出来的。

即，椭圆曲线除了方程式参数a、b以及基点G，还有另外两个重要的参数素数P和子群的阶n，它们决定了一条椭圆曲线上的哪些点可以在ECC相关算法中使用:

  • 素数P : ECC不是直接使用椭圆曲线上的点，而是将方程式对一个素数P进行模运算来转换成一个有限域 : y^2 ≡ x^3 + ax + b (mod P) , x,y ∈ [0, P]，这个有限域的元素的个数就是P，P是一个素数。这个方程的意思是，y^2和(x^3 + ax + b)对P同余， 即它们对P做求模运算的结果是一样的。在求模之前，椭圆曲线上的点坐标，y值是相对x轴(y=0)这条线对称的，求模转换之后，曲线上的点的坐标，y值相对y=P/2这条线对称。此时椭圆曲线变成了一些离散的点，它们可能是这样子的:
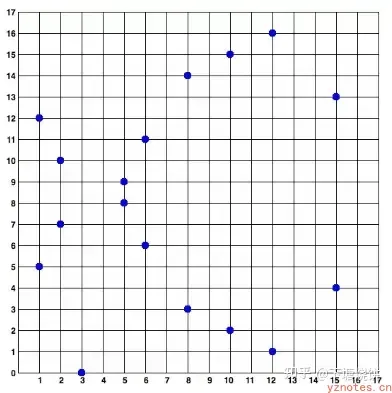
ECC子群
ECC子群

ECC子群

  • 子群阶n : 素数P求模运算的结果是一个比椭圆曲线上所有点更小的数集，叫做群，然后曲线上从基点G开始的打点操作会生成一个更小的子群。这个子群中元素的个数，就是子群的阶n。对ECC来说，总是希望子群拥有更高的阶。实际上是先计算椭圆曲线的阶N，找一个比较大的因子n，然后根据n找出一个合适的基准点。也就是说，实际在寻找合适的椭圆曲线参数时，是先找子群的阶，再根据子群的阶找其中的基准点。而不是先找基准点，再算子群的阶。在计算基点时，除了N还用到了另一个参数:子群的协因子(cofactor), 通常简写为h。

综上，一般来说，一个ECC会有以下6个参数:

  • a : 椭圆曲线方程参数a
  • b : 椭圆曲线方程参数b
  • p : 一个素数，椭圆曲线上的有限域的大小
  • n : 子群的阶，即子群的大小
  • xg : 基点G的x轴坐标
  • yg : 基点G的y轴坐标

2.1.3 常见的椭圆曲线

设计某个ECC时，需要先设计一条安全的椭圆曲线，然后选择一个基点G。这种曲线通常并不是自己设计的，因为设计上要满足上述特性很有难度。

目前国际上常用的ECC曲线主要是NIST系列曲线，它是由美国的国家标准技术研究所制定的系列ECC曲线，包括P-256、P-384、P-521等等，目前被业界怀疑植入了后门。

我国的国家标准也推出了自己的ECC曲线: SM2-P-256。

此外，由于大家都怀疑NIST，很多语言和开源社区都在推动Curve25519、Curve448等并非基于维尔斯特拉斯标准形式的椭圆曲线，所以现在越来越多的语言都内置了Curve25519的实现，比如golang的crypto/ed25519包，java对Ed25519的支持等等。

著名的开源ssl工具openssl支持很多种椭圆曲线，可以用命令openssl ecparam -list_curves查看openssl支持的ECC椭圆曲线，其中:

  • prime256v1对应NIST的P-256
  • secp384r1对应NIST的P-384
  • secp521r1对应NIST的P-521
  • SM2对应中国国家标准的SM2-P-256

openssl也支持Curve25519等非维尔斯特拉斯标准形式曲线，但无法在上述命令结果中找到，可以使用openssl genpkey -algorithm x25519命令生成一个使用Curve25519曲线的私钥。

本篇笔记使用的openssl版本: OpenSSL 3.0.1

2.2 基于ECC的密钥交换算法ECDH与ECDHE

ECDH是Elliptic Curve Diffie-Hellman，它一种基于ECC的密钥协商算法。

ECDH是笛福赫尔曼(Diffie-Hellman)算法的变种，它是一种密钥协商协议，定义了密钥怎么样在通信双方之间生成和交换。其思路过程与笛福赫尔曼密钥协商算法基本相同，只是在具体的协商计算中使用ECC。因此我们直接学习ECDH也就相当于学习了笛福赫尔曼(Diffie-Hellman)算法。

ECDH的过程如下:

  1. A和B生成各自的私钥和公钥，A的私钥为da，公钥为Ha 。B的私钥为db，公钥为Hb。注意，A和B需要使用同样的椭圆曲线与基点G。
  2. A和B通过不安全信道交换各自的公钥Ha和Hb，中间人可以窃听到Ha和Hb，但是在无法攻破离散对数难题的情况下无法得到da和db。
  3. A计算S=da*Hb（使用自身的私钥和 B 的公钥），B计算S=db*Ha（使用自身的私钥和 A 的公钥），双方求得的 S 是一样的，因为S=da*Hb=da*(db*G)=db*(da*G)=db*Ha。S就是双方协商好的新密钥。这里的*依然是打点操作的乘法。

这个过程可以用下图表示:

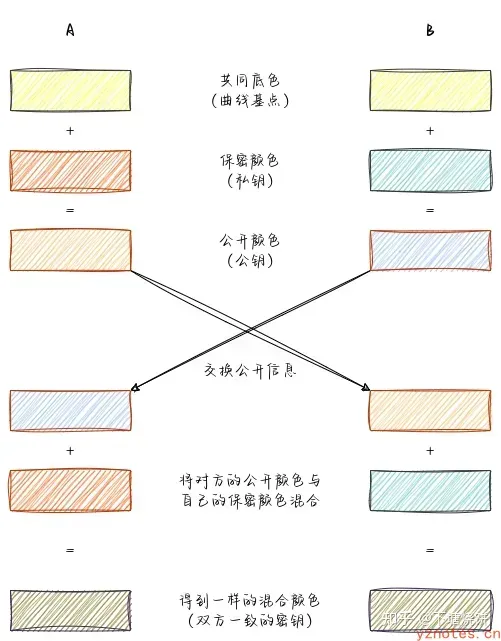
ECDHE是基于ECDH添加了动态功能的密钥协商算法。ECHDE 中的 E 代表着ephemeral, 短暂的，是指交换的密钥是暂时的动态的，而不是固定的静态的。比如tls协议中，每次建立新连接时，服务器和客户端都会动态生成新的公私钥，这些动态的公钥通过ECDH进行交换，之后会用于双方协商预主密钥，进而生成会话密钥。

2.3 基于ECC的签名算法ECDSA

ECDSA是Elliptic Curve Digital Signature Algorithm，基于椭圆曲线的数字签名算法。

ECDSA在基于ECC生成公私钥对之后，使用私钥签名，使用公钥验签。

前提：

  1. 基于ECC生成公私钥对：私钥d、公钥H。
  2. 对签名内容进行散列摘要，得到 z。事先做摘要的目的主要是在确保内容唯一性的前提下，减少签名内容，降低私钥签名运算消耗，减少签名结果长度。(通常签名内容越长，签名结果也就越长。)

签名过程(注意签名使用的是私钥d，不使用公钥H)：

  1. 选取一个[1, n-1]之间的随机数k，n是子群的阶n，随机数算法建议使用CSPRNG，注意这里的k不是私钥。
  2. 通过打点操作P = k * G计算曲线上的另一个点P，G是曲线基点，注意P不是公钥。
  3. 计算数字r = P(x) mod n，P(x)是P的x轴座标，如果r为0，则重新选取随机数k，再来一次。
  4. 利用私钥d，对签名内容的摘要z做计算: s = (k^-1)(z + rd) mod n，如果s为0，则重新选取随机数k，再来一次。
  5. (r,s)就是签名。

验签过程(注意验签使用的是公钥H，不使用私钥d)：

  1. 计算整数 u1 = (s^-1)z mod n
  2. 计算整数 u2 = (s^-1)r mod n
  3. 计算点P = u1 * G + u2 * H
  4. 判断 r == P(x) mod n ，相等则验证成功

三、SM2相关算法

SM2是我国国家标准的基于维尔斯特拉斯标准形式椭圆曲线的公钥密码学算法，可以参考国标GB/T 32918.1-2016 。

SM2也是一种ECC，选择了一条自己的曲线SM2-P-256，并在此基础上，提供了数字签名、密钥交换与非对称加密算法。具体可以参考国家标准文档:

https://openstd.samr.gov.cn/bzgk/gb/std_list?p.p1=0&p.p90=circulation_date&p.p91=desc&p.p2=GB/T%2032918open in new window

相关标准分别是:

  1. GB/T 32918.1-2016 SM2椭圆曲线公钥密码算法 第1部分：总则 (发布日期:2016-08-29)
  2. GB/T 32918.2-2016 SM2椭圆曲线公钥密码算法 第2部分：数字签名算法 (发布日期:2016-08-29)
  3. GB/T 32918.3-2016 SM2椭圆曲线公钥密码算法 第3部分：密钥交换协议 (发布日期:2016-08-29)
  4. GB/T 32918.4-2016 SM2椭圆曲线公钥密码算法 第4部分：公钥加密算法 (发布日期:2016-08-29)
  5. GB/T 32918.5-2017 SM2椭圆曲线公钥密码算法 第5部分：参数定义 (发布日期:2017-05-12)

公钥加密算法即非对称加密算法。

3.1 SM2椭圆曲线与公私钥

SM2的椭圆曲线方程采用维尔斯特拉斯标准形式： y^2 = x^3 + ax + b 且 4a^3+27b^2!=0。

SM2选择如下的曲线参数，即，SM2设计了一条自己的曲线：SM2-P-256，一个素数域256位椭圆曲线。

p=FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF
a=FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC
b=28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93
n=FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123
Gx=32C4AE2C1F1981195F9904466A39C9948FE30BBFF2660BE1715A4589334C74C7
Gy=BC3736A2F4F6779C59BDCEE36B692153D0A9877CC62A474002DF32E52139F0A0

这里有个数学上的优化： 本来按照标准给定的参数a的值是FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC， 注意这个值其实就是p-3，即a = p-3。 将a = p-3带入对P求模运算的公式: y^2 ≡ x^3 + ax + b (mod p)，可以得到一个更简单的方程式，计算过程如下:

x^3 + ax + b (mod p)
=(x^3 + ax + b) % p
=(x^3 + (p-3)x + b) % p
=(x^3 + px-3x + b) % p
=(x^3 %p + px %p -3x %p + b%p) % p            // 此处遵循模运算分配率: (a+b)%p=(a%p+b%p)%p
=(x^3 %p + (p%p * x%p) %p -3x %p + b%p) % p   // 此处遵循模运算分配率: (a*b)%p=(a%p * b%p)%p
=(x^3 %p -3x %p + b%p) % p                    // 对自己求余结果是0, 0对任何数求余也还是0, 故 p%p =0, 故 (p%p * x%p) %p = 0
=(x^3 - 3x + b) % p                           // 逆用分配率

即最终求模后的方程可以变为: y^2 ≡ x^3 - 3x + b (mod p)

SM2的公私钥生成与其他ECC一样，这里不再赘述。以go为例，其公私钥的数据结构如下所示:

// 公钥结构
type PublicKey struct {
    elliptic.Curve // 椭圆曲线
    X, Y *big.Int  // 公钥座标
}
// 私钥结构
type PrivateKey struct {
    PublicKey  // 公钥
    D *big.Int // 私钥，随机数d
}

公钥长度: 64Byte，即512位。x与y转为字节数组后，需要分别补充到32字节。 私钥长度: 32Byte，即256位。随机数转为字节数组后，需要补充到32字节。

3.2 SM2数字签名

SM2的数字签名算法与ECDSA并不相同，不仅仅是椭圆曲线参数不同，算法本身亦不相同。详细的算法请参考国标文件GB/T 32918.2-2016。

SM2的签名算法也是在基于SM2曲线生成公私钥对之后，使用私钥签名，使用公钥验签。

前提:

  • 基于SM2生成公私钥对: 私钥d、公钥H

注意，SM2并不要求一定要事先对签名内容做散列摘要，因为SM2算法内部已经设计了散列过程。当然事先做一下也没问题。

SM2签名过程(私钥签名):

  1. ZA运算，通过公式SM3(ENTLA || IDA || a || b || xG || yG || xA || yA)计算ZA, ZA是一个散列用的盐值，该盐值混入了一些曲线参数(a,b,xG,yG)以及公钥的座标(xA,yA)，IDA是用户唯一标识，ENTLA是IDA的比特位数转换而来的两个字节。
  2. 对签名内容进行SM3(ZA || M)摘要计算(混入ZA)，M是签名内容，然后将摘要转换为数字e。
  3. 生成随机数k，位于[1,n-1]区间，n是子群的阶，随机数算法建议使用CSPRNG，注意这里的k不是私钥。。
  4. 计算 P = k*G ，得到曲线上另一个点P，G是基点，注意P不是公钥。
  5. 计算 r = (e + P(x)) mod n, P(x)是P的x轴坐标。
  6. 计算 s = (((1 + d)^-1) (k-rd)) mod n。
  7. (r,s)就是签名。

最大签名数据量长度无限制，签名结果为64字节(r + s)，但由于签名后会做ASN.1编码，实际输出长度为70-72字节。

SM2验签过程(公钥验签):

  1. ZA运算，SM3(ENTLA || IDA || a || b || xG || yG || xA || yA)，与签名时相同。
  2. 对签名内容进行SM3摘要计算(混入ZA)，并根据摘要值得到数字e，与签名时相同。
  3. 计算 t = (r + s) mod n，根据签名结果计算中间结果t。
  4. 计算 P = s*G + t*H，根据公钥H，以及签名结果s，以及中间计算结果t计算P点坐标。
  5. 计算 R = (e + P(x)) mod n，根据P(x)与e计算新的R。
  6. 判断 R == r，比较新计算出的R是否与签名结果r相同。

与ECDSA相比，SM2的签名算法有以下不同:

  1. 曲线不同。ECDSA一般使用NIST曲线，支持多种曲线如P256、P521等等，而SM2使用的是SM2-P-256曲线。
  2. 签名内容是否需要事先散列的要求不同。ECDSA需要事先对签名内容做散列，而SM2则没有该要求，并在算法内部提供了对签名内容的加盐散列。
  3. 签名与验签的计算公式不同，包括签名时r与s的计算公式以及验签时相关值的计算公式。

3.3 SM2密钥交换

SM2的密钥交换算法与ECDH的基本过程是一样的，但是相关计算公式更加复杂。详细的算法请参考国标文件GB/T 32918.3-2016。

SM2的密钥交换主要是在拿到对方的公钥后，并不是简单的用打点运算得到新的密钥，而是通过一系列设计好的数学公式，KDF密钥派生等操作来协商出新密钥。

具体的计算公式比较复杂，这里偷个懒，不记笔记了。。。

3.4 SM2公钥加密

与前面介绍的一般的ECC不同，SM2除了签名与密钥交换，还提供了公钥加密算法，即非对称加密算法。详细的算法请参考国标文件GB/T 32918.4-2016。

SM2加密过程(公钥加密):

  1. 获取随机数k，位于[1,n-1]区间，n是子群的阶，随机数算法建议使用CSPRNG，注意这里的k不是私钥。
  2. 计算点C1 = k*G ，因为k是随机数，所以C1每次加密都是随机的, C1的目的是将随机数k隐藏在其中，其他人截获了C1并不能根据G倒推出k。
  3. 计算点P(x2,y2) = k*H, 对公钥H做k此打点，得到新的点P。P是实际加密需要使用的一个参数，可以认为是预密钥，P在解密时可以根据C1*私钥d得到。
  4. 计算C3 : 按 x2+data(明文)+y2 的顺序混合数据并做SM3摘要, C3是为了认证而做的加盐散列，盐值就是P，x2和y2是P的坐标。
  5. 使用密钥派生函数kdf，基于P计算长度等于data长度的派生密钥key。kdf是一个基于SM3的密钥派生函数。
  6. 计算C2，利用key对data进行异或运算，得到的密文即C2, 为什么是异或运算，因为用相同的值连续做两次异或运算就得到了原值，适合用来加解密。
  7. 根据模式C1C3C2或C1C2C3拼接最终的密文。

模式：C1C3C2 与 C1C2C3 只是拼接顺序不同，具体C1、C2、C3的内容是一样的。

  • C1: sm2椭圆曲线上的某个点，每次加密得到的点不一样，x和y座标轴各转为32个字节，因此C1长度为64字节。有时要对C1坐标值做压缩，此时会在C1前面加一个标识用字节，值固定为0x04，此时C1长度变为65个字节。
  • C2: 密文，根据公钥随机打点得到随机点P，再根据P通过密钥派生函数kdf计算一个与明文字节流等长的密钥ct，使用该ct与明文进行异或加密运算得到的密文。
  • C3: 随机点P与明文混合后的sm3摘要，混合顺序：Px+data+Py，长度为32字节。

支持明文最大近128G字节，加密结果在明文字节数的基础上，增加了96字节(C1:64字节, C3:32字节)，如果首个字节为0x04则增加97字节，实际有效96字节。

SM2解密过程(私钥解密):

  1. 取出C1
  2. 根据C1计算 P = d*C1, 这里计算出来的P就是加密时计算的P，因为 P=d*C1=d*k*G=d*G*k=H*k
  3. 使用密钥派生函数kdf，基于P计算派生密钥key
  4. 使用派生密钥key对C2部分做异或计算解密得到明文
  5. 重新混合明文并计算摘要，与C3进行比较

四、Curve25519相关算法

前面说过，椭圆曲线不仅仅只有维尔斯特拉斯标准形式，还有蒙哥马利曲线(Montgomery Curve)、扭曲爱德华曲线(Twisted Edwards Curve)等。其中，蒙哥马利曲线和扭曲爱德华曲线可以相互等价转换。由于NIST曲线的后门问题，越来越多的语言与开源社区开始推广使用蒙哥马利曲线Curve25519的相关算法：

  • x25519密钥交换算法 : 过程与ECDH基本相同，但曲线改为Curve25519曲线。
  • ed25519数字签名算法 : 使用EdDSA签名算法，曲线使用从Curve25519等价变换来的扭曲爱德华曲线Edwards25519，散列使用SHA-512算法。

除了Curve25519，还有在安全性上更好但性能上更慢的Curve448曲线，这里就不关注了。

4.1 x25519密钥交换算法

x25519是一种密钥交换算法，算法就是ECDH，但其椭圆曲线使用Curve25519。

Curve25519椭圆曲线方程为：y^2 = x^3 + 48662 x^2 + x。

x25519生成公私钥的算法与ECC一样，交换密钥算法过程与ECDH相同，不再赘述。

4.2 ed25519数字签名算法

ed25519是一种数字签名算法，其曲线、公私钥生成、数字签名算法都与前面学习的ECC相关算法不同。

  • ed25519使用的椭圆曲线是Edwards25519，一种从Curve25519等价变换来的扭曲爱德华曲线: -x^2 + y^2 = 1 - (121665/121666) x^2 y^2。
  • ed25519的公私钥生成与ECC并不完全一样，公钥并不是直接使用私钥打点计算得来。
  • ed25519的数字签名算法采用的是EdDSA算法，与ECDSA并不相同。

其数字签名算法过程大致如下:

STEP1 生成公私钥

  1. 随机数发生器生成随机数d作为私钥。
  2. 计算私钥的摘要(使用SHA-512)，并通过一个数学公式进行运算，得到一个整数a和一个随机数k。
  3. 计算公钥:Y = a * G，G是曲线基点，Y是公钥。

STEP2 签名

  1. 计算r : r = H(k, M)， H是散列算法SHA-512，k是生成公私钥时生成的随机数。
  2. 计算曲线上一个新的坐标点R : R = r * G。
  3. 计算s : s = (r + H(R, Y, M)a) mod l，l是一个质数，满足l * G = 0。
  4. (R, s)就是签名。

STEP3 验签

验证s * G = R + H(R, Y, M)Y是否成立即可。

4.3 Curve25519的优势

Curve25519相关算法具备以下优势:

  1. 完全开放设计，算法各参数的选择直截了当，非常明确，没有任何可疑之处。相比之下目前广泛使用的NIST系列曲线，其方程参数是由来历不明的随机种子c49d3608 86e70493 6a6678e1 139d26b7 819f7e90生成的，至于这个种子的来历没有资料介绍。
  2. 安全性高，25519系列椭圆曲线经过特别设计，一般认为在安全性上比NIST系列曲线更高。
  3. 速度快，25519系列椭圆曲线算法的性能超过大部分NIST系列曲线。

五、RSA简介

RSA是一种目前仍在大量使用，但安全性遭到一定的质疑，正在被ECC慢慢取代的公钥密码系统。

它的数学理论是大整数因数分解难题，其生成公私钥的过程简单描述如下:

  1. 随机选择两个不相等的质数p和q。这两个质数越大，RSA就越难破解。
  2. 计算p和q的乘积n。n的二进制位数就是密钥长度，目前生产上满足安全要求的话，n需要达到2048位。
  3. 计算n的欧拉函数φ(n)。所谓欧拉函数就是计算这样一个问题的函数:在小于等于n的正整数之中，有多少个与n构成互质关系。
  4. 随机选择一个整数e，条件是1< e < φ(n)，且e与φ(n) 互质。实际应用中经常选择65537。
  5. 计算e对于φ(n)的模反元素d。所谓模反元素就是指有一个整数d，可以使得ed和1对φ(n)同余，即ed ≡ 1 (mod φ(n))，也即ed对φ(n)求余为1。
  6. 将n和e封装成公钥:(n,e)，n和d封装成私钥:(n,d)。

RSA与SM2一样，同时提供了签名、密钥交换与非对称加密算法。

  • RSA非对称加密很简单。使用公钥加密:m^e ≡ c (mod n)，m是明文，n和e是公钥，c是加密后的密文。解密则是c^d ≡ m (mod n)，d和n是私钥。
  • RSA签名更简单。就是对明文做散列计算得到摘要后，用私钥加密摘要(就是RSA非对称加密的加密公式)得到签名。验签时用公钥解密得到摘要与明文摘要值比对。
  • RSA密钥交换还是很简单。比如通信双方是A与B，A将自己的RSA公钥发给B，B生成一个伪随机数作为密钥，用A的公钥加密，再发给A，A再用自己的私钥解密，得到客户端生成的密钥。

注意，RSA的公私钥貌似可以互换使用，但在实际中不可以这样做。因为RSA的公钥e和私钥d的密码学安全性是不一样的，暴露e，很难破解出d，但暴露d出去，则e相对容易被破解。

不论RSA还是ECC，如果是非对称加密，一定是公钥加密，私钥解密；如果是签名，一定是私钥签名，公钥验签。这是由加密和签名的不同的需求决定的。 公钥是公开的，所有人都可以拿到，而私钥是只有自己才能持有的，不可泄露。 非对称加密场景，某人发消息给B，某人要确保这个消息只有B能解密，因此必须用B的公钥加密，这样就只有B的私钥持有者(即B自己)才能解密看到消息。 签名场景，A发消息给别人，别人收到消息时需要确保这个消息是A发来的，因此A需要使用自己的私钥对消息进行签名，这样别人收到消息时可以用A的公钥来验签，确保这个消息确实是A发送的。

RSA的非对称加密与签名，只要密钥长度足够(2048位以上)，那么目前仍然认为它是安全的。但RSA的密钥交换算法则被认为不够安全，比如tls1.3协议中，就已经废弃了对RSA密钥交换算法的支持，改为使用ECDHE密钥交换算法。

六、SSH密钥登陆

公钥密码学有很多使用场景，这里我们先看一个简单的应用: ssh的密钥登陆，或者说免密登录，这里的免密是指不用输入账户密码。

对于一个linux服务器运维人员来说，使用ssh客户端工具连接linux服务器是日常操作。有时运维人员会将目标服务器的账户密码保存在ssh客户端工具，避免每次ssh连接是都要输入用户和密码。但更方便也更安全的做法是，不使用账户密码登陆，而是利用公钥密码系统的数字签名算法实现SSH免密登陆。

使用流程如下:

  1. 在客户端生成一套公私钥，比如使用ssh-keygen工具生成一对ed25519的公私钥: ssh-keygen -t ed25519，命令过程中一路回车即可，结果可以在~/.ssh中看到ed25519的私钥文件id_ed25519和公钥文件id_ed25519.pub。
  2. 将公钥文件拷贝到目标Linux服务器，比如ssh-copy-id -i ~/.ssh/id_ed25519.pub root@x.x.x.x，该命令会将本地的公钥文件id_ed25519.pub的内容追加写入目标服务器的root用户根目录的~/.ssh/authorized_keys文件，该文件是可信任列表，存放所有可信任的客户端公钥。
  3. 此时从客户端就可以直接ssh免密登陆目标Linux服务器: ssh root@x.x.x.x。

上述流程生成公私钥使用的是ed25519，也可以使用rsa，或ecdsa。

ssh的密钥登陆的认证流程则如下:

  1. 客户端发送ssh连接请求，并携带自己的公钥。
  2. 服务端检查客户端发来的公钥是否在自己的authorized_keys可信任列表中，若存在，则生成一些随机数返回给客户端。
  3. 客户端收到服务端返回的随机数，用私钥签名，将签名结果发给服务端。
  4. 服务端收到签名，用对应的公钥验签，验签OK则通过认证。

无论是安全性还是性能，ed25519都是目前ssh支持的密钥类型中最优秀的，但有些比较老的linux服务器上的ssh的版本可能会比较老，不支持ed25519，所以目前使用rsa的ssh密钥也依然很多。

七、小结

公钥密码学的理论基础是基于数学难题的公私钥难以被攻破，目前主流的公钥密码系统是ECC椭圆曲线密码学，通常提供了密钥交换算法(ECDH/ECDHE)与数字签名算法(ECDSA)。SM2是国标的ECC，使用自己的维尔斯特拉斯标准形式椭圆曲线，提供了自己的密钥交换算法、数字签名算法、非对称加密算法。Curve25519是各大社区与语言极力推广的蒙哥马利曲线，x25519就是ECDH使用Curve25519的密钥交换算法，ed25519是Curve25519等价变化的扭曲爱德华曲线，只提供数字签名算法EdDSA，算法具体实现与ECDSA不同。

接下来，继续学习各种密码学算法在互联网环境下的应用(特别是公钥密码学):

默认页脚
Copyright © 2024 gong_yz